A major focus of our research is the development of higher-order, adaptive finite element methods for the numerical solution of partial differential equations (PDEs).  The numerical error from approximating a PDE is controlled by the mesh used to discretize the domain.  If the mesh is sufficiently fine in regions of the domain that have a significant impact on the error in the solution, then the numerical solution will be an accurate approximation of the exact solution of the PDE.  However, most numerical simulations conducted today are very complex. As a result, it is difficult to know a priori all of the regions which require fine mesh resolution.  An example of how numerical errors have had a significant impact on an engineering design is the Sleipner A offshore oil platform which collapsed during final construction and later investigation showed the cause to be inaccurate finite element structural analysis. 

The key idea behind an adaptive method is to approximate the PDE on an initial mesh, and then utilize a quantifiable estimate of the error to algorithmically adapt the mesh.  This adaptive process can then be iterated to further reduce the numerical error.  This algorithmic control of numerical error can significantly reduce the risk associated with making incorrect scientific or engineering decisions based on inaccurate simulation of PDE models.

The specific adaptive approach we frequently use is referred to as output-based adaptation (also known as goal-oriented adaptation).

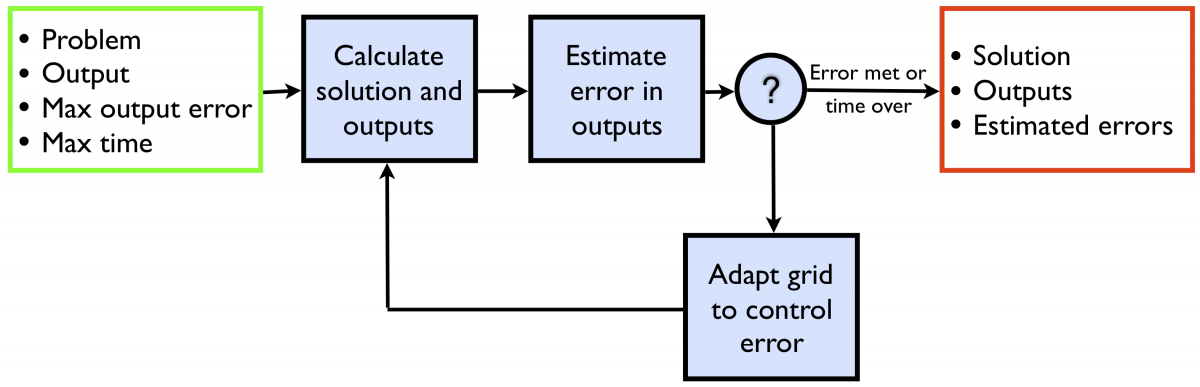
An output is a quantity that is a key result from the simulation, for which there exists a maximum predictive error.  Some examples of outputs in different applications are:

• Aerodynamics: lift or drag acting on an airplane.
• Groundwater contaminatiion: total flow of a pollutant in water
• Weather prediction: maximum sustained winds from a hurricane
• Propulsion: efficiency of a jet engine
• Structural design: critical load leading to structural failure 

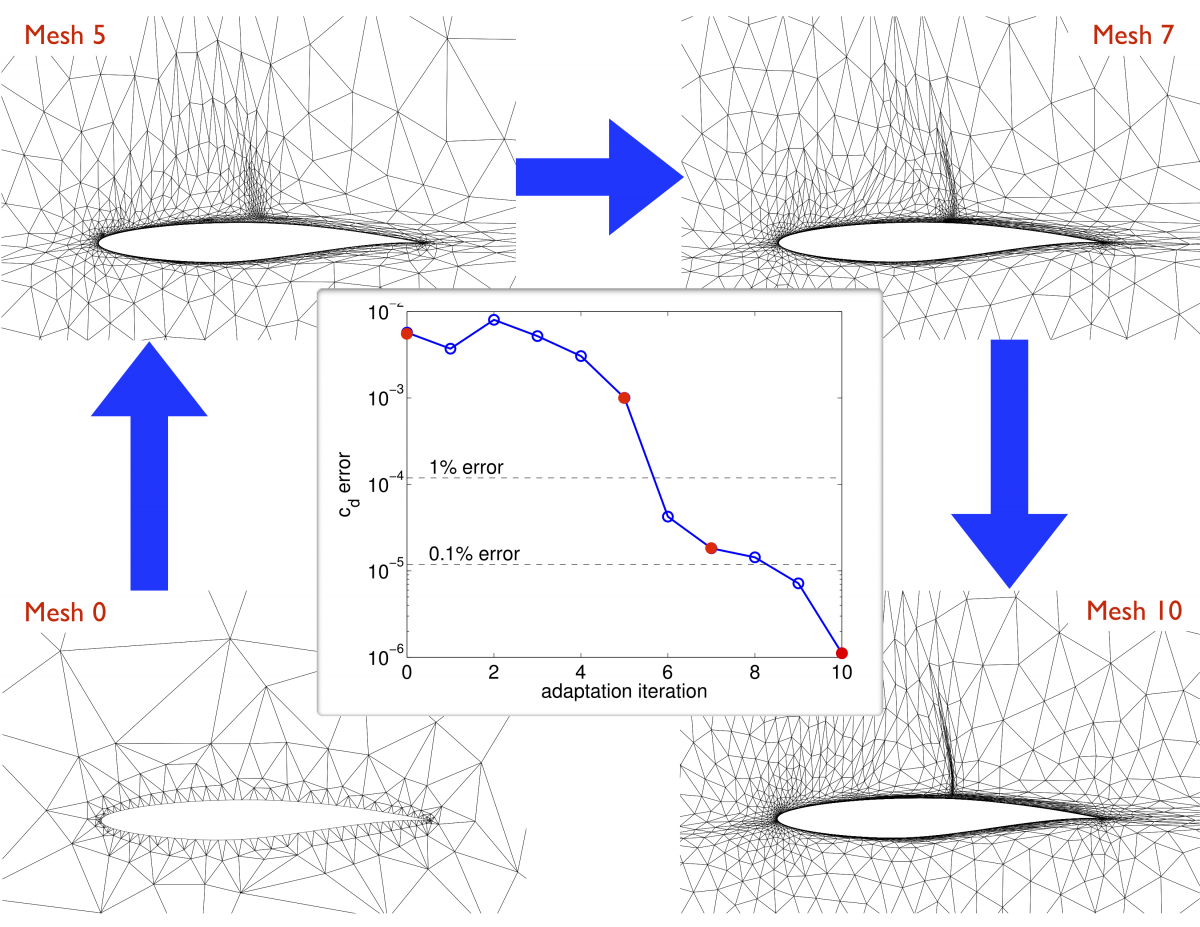
The image below shows the convergence of our output-based adaptation algorithm applied to a transonic flow over the RAE 2822 airfoil modeled with the Reynolds-Averaged Navier-Stokes (RANS) equations and Spalart-Allmaras (SA) turbulence model and discretized with a discontinuous Galerkin FEM.  Starting from a very coarse initial mesh, the adaptive process converges to a mesh with around 0.01% error in the drag.

The following video shows the evolution of meshes using our adaptive algorithm to simulate the transonic RANS flow over a NACA 0012.

 

For more information about this research, try the following links:

• Overview of MOESS adaptive algorithm
• Impact of adaptation on accuracy of higher-order methods
• Comparison of different finite element methods
• SANS software that implements our higher-order adaptive finite element method